Stability–Quality Paradox in Decentralized Diffusion Models

Why the most stable samplers in decentralized diffusion produce the worst generations

In Decentralized Diffusion Models (DDMs), denoising is routed through independently trained experts at inference time. These experts can strongly disagree in their denoising predictions. What actually governs the quality of generations in such a system? We present the first ever systematic interpretability study of this question.

The natural expectation is that minimizing denoising trajectory sensitivity — minimizing how perturbations amplify during sampling — should govern generation quality. It doesn’t. Full ensemble routing, which combines all expert predictions at each step, achieves the most stable sampling dynamics and the best numerical convergence. It also produces the worst generation quality (FID 47.9 vs. 22.6 for sparse Top-2 routing). We call this the stability–quality paradox.

Instead, we identify expert-data alignment as the governing principle. Generation quality depends on routing inputs to experts whose training distribution covers the current denoising state, even when doing so makes the trajectory unstable. For DDM deployment, routing should prioritize expert-data alignment over the usually used numerical stability metrics.

---

Decentralized Diffusion Models

DDMs aren’t Mixture-of-Experts layers. They’re ensembles of independently trained models. In standard MoE architectures, experts are FFN layers within a shared backbone, trained jointly with load balancing losses, and routed at the token level. DDM experts are complete diffusion models, and routing occurs at the input level (entire noisy generations) rather than token level.

Training

Each expert trains in isolation on a disjoint data partition. The training data is partitioned into K clusters (e.g., using k-means on DINOv2 embeddings), and each expert sees only its assigned cluster. So one might train exclusively on landscapes, another on portraits. No shared parameters or gradient communication. Experts only collaborate at inference time.

MoE experts, therefore, operate within a shared representational framework that limits their differences. In contrast, DDM experts are unrestricted and can generate vastly different outputs from the same input.

Routing

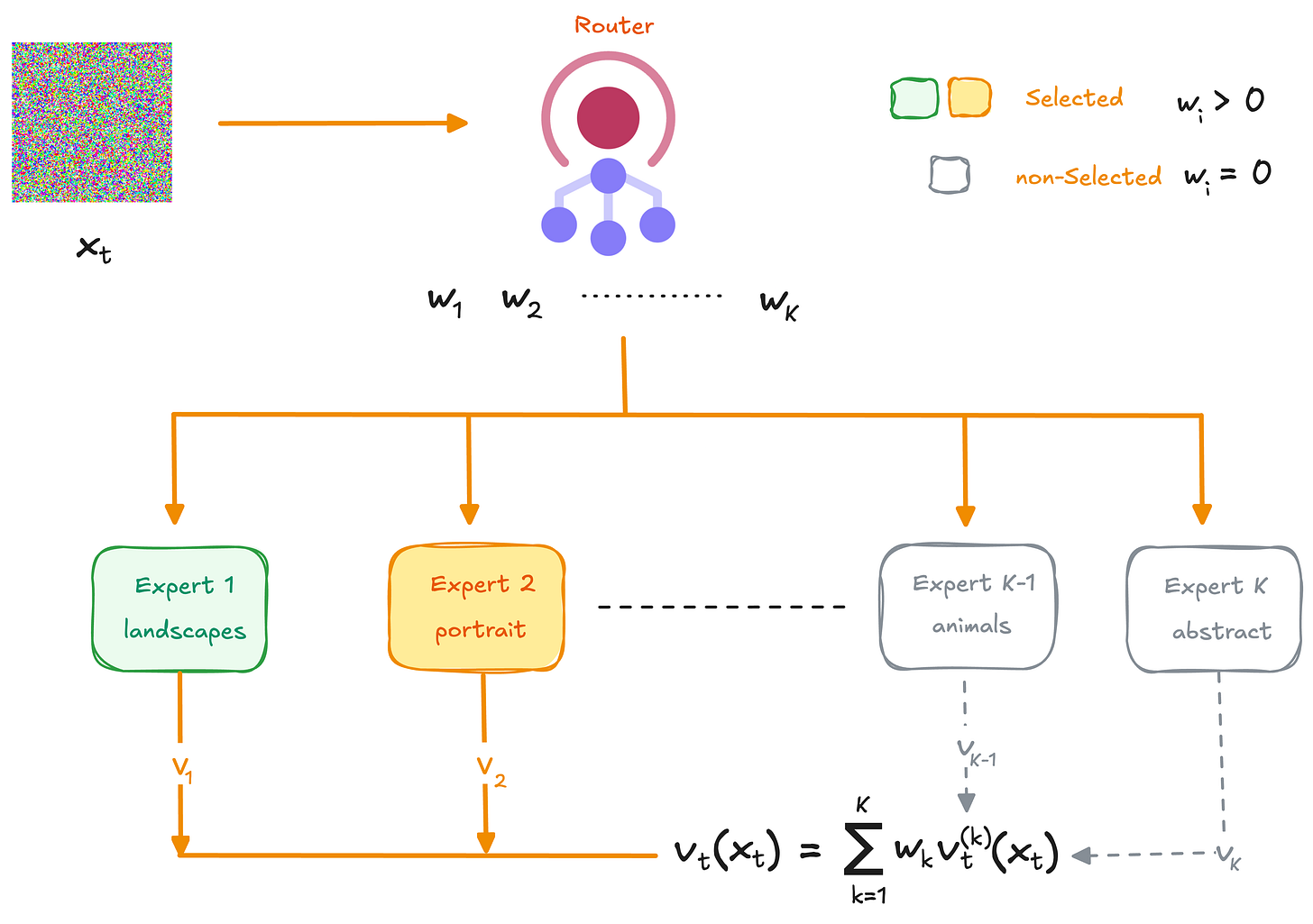
At inference time, a lightweight router predicts weights

\(w_t^{(k)}(x_t) \geq 0 \quad\text{with}\quad \sum_{k=1}^K w_t^{(k)}(x_t) = 1\)

at each denoising step. The routed velocity field is:

\(v_t(x_t) = \sum_{k=1}^K w_t^{(k)}(x_t) \cdot v_t^{(k)}(x_t).\)

The critical design question is how many experts should contribute at each step. Three natural strategies emerge.

Top-1 commits fully to the single most relevant expert. Every prediction comes from one model. If the router picks poorly, there’s no fallback.

Top-2 blends the two most relevant experts after renormalizing their weights. This allows experts to cross-check each other while still filtering out the majority.

Full Ensemble weights all experts by their router probability. Every expert contributes to every step, giving the mathematically complete combination.

Standard numerical analysis would suggest that including more experts should help. Averaging reduces variance, smooths the velocity field, and stabilizes the ODE integration. We tested whether this intuition holds.

---

The Stability Paradox

Numerical stability has been the default lens for optimizing diffusion sampling. The foundational probability-flow ODE formulation frames Lipschitz constants and discretization error as determining solver accuracy. Recent work develops stabilized Runge-Kutta methods for stiff diffusion ODEs, studies Lipschitz singularities and their effects on sampling, and the entire solver design space from Euler to Heun to DPM++ is organized around stability-accuracy tradeoffs. These analyses target single-model diffusion, and DDM-specific stability analysis did not exist. We provide the first systematic test of whether this framework transfers to distributed training systems.

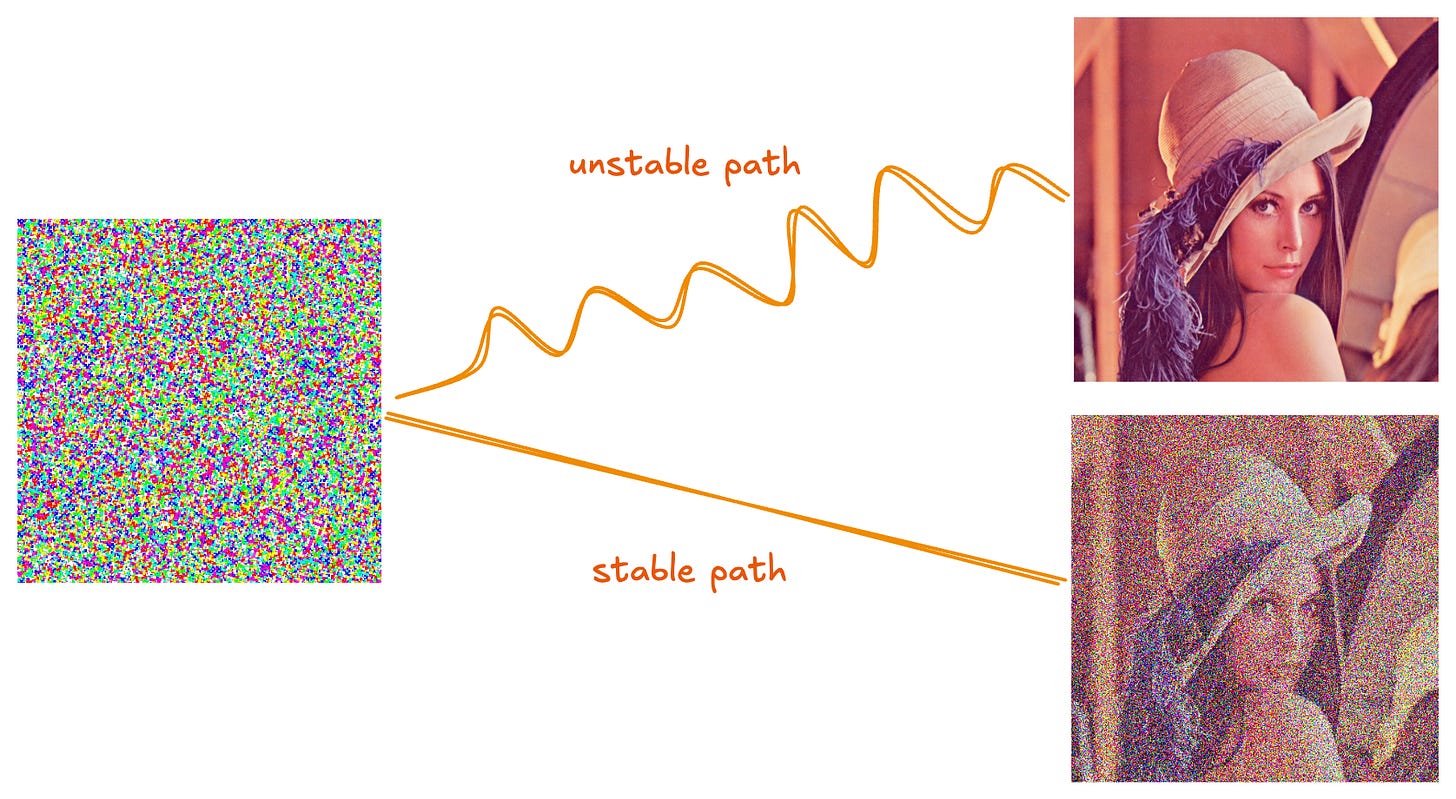
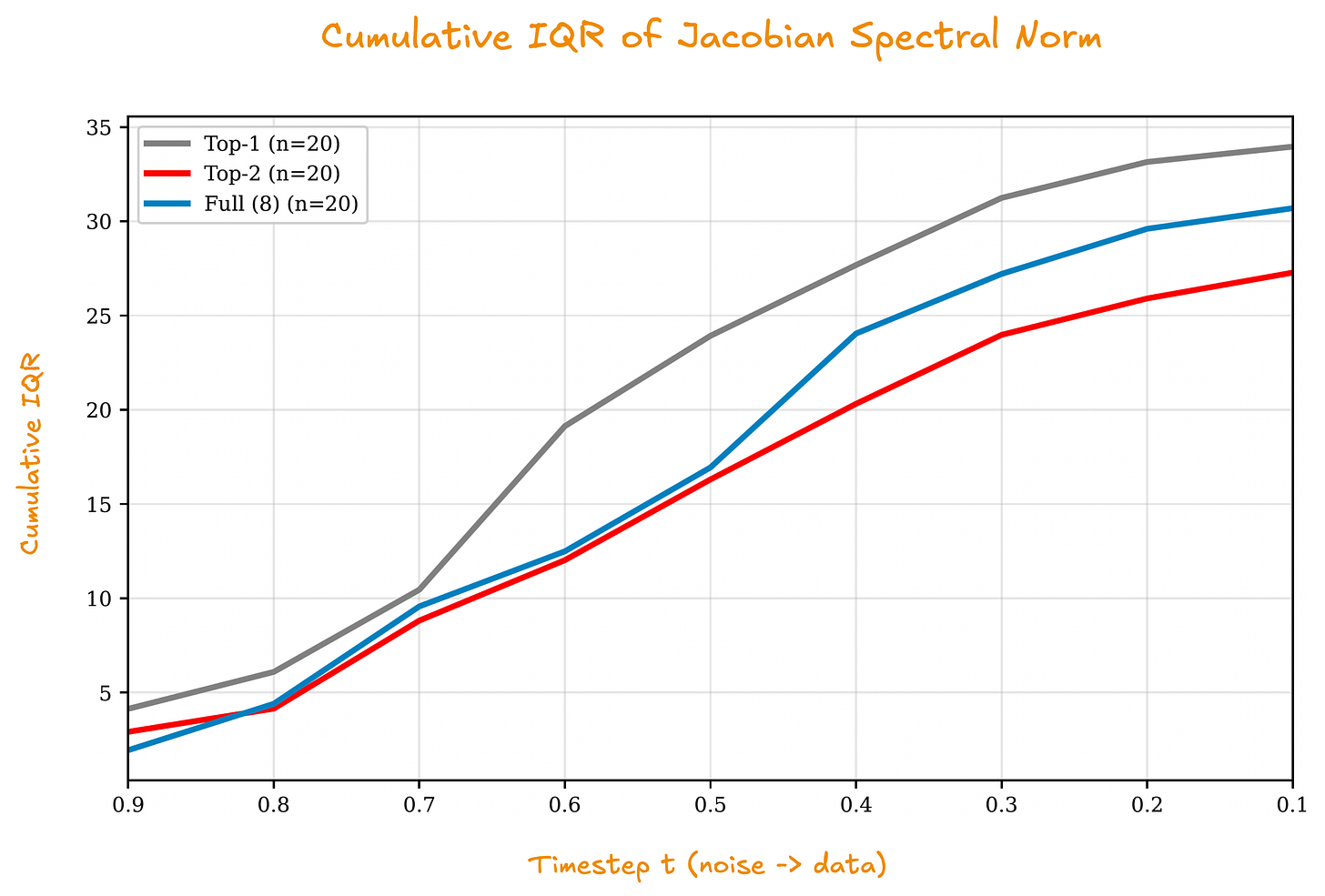
We evaluated on Paris, the world’s first publicly released DDM, comprising 8 experts trained on LAION-Aesthetics. We tracked trajectory sensitivity, measuring how strongly the velocity field responds to input perturbations, and step-refinement disagreement, the difference between images generated with N and 2N steps. The results reveal a stability–quality paradox.

\(\begin{array}{lccc} \hline \text{Routing Strategy} & \text{FID }\downarrow & \hat{L}_{eff}^{(h)}\downarrow & \Delta_{refine}\downarrow \\ \hline \text{Top-2 (Sparse)} & \mathbf{22.60} & 17.48 & 0.051 \\ \text{Full Ensemble} & 47.89 & \mathbf{17.07} & \mathbf{0.020} \\ \hline \end{array}\)

Full Ensemble achieves the lowest trajectory sensitivity. It converges the most cleanly. And it produces the worst images, with FID nearly double that of Top-2.

The cumulative IQR measures variability across denoising trajectories. Full Ensemble shows the lowest variability, indicating consistent, well-behaved numerical integration. Top-2 shows higher variability, yet produces superior images. For full experimental details, see the full paper.

Why does averaging more experts — which stabilizes the denoising trajectory degrade image quality?

---

Expert-Data Alignment Is The Governing Principle

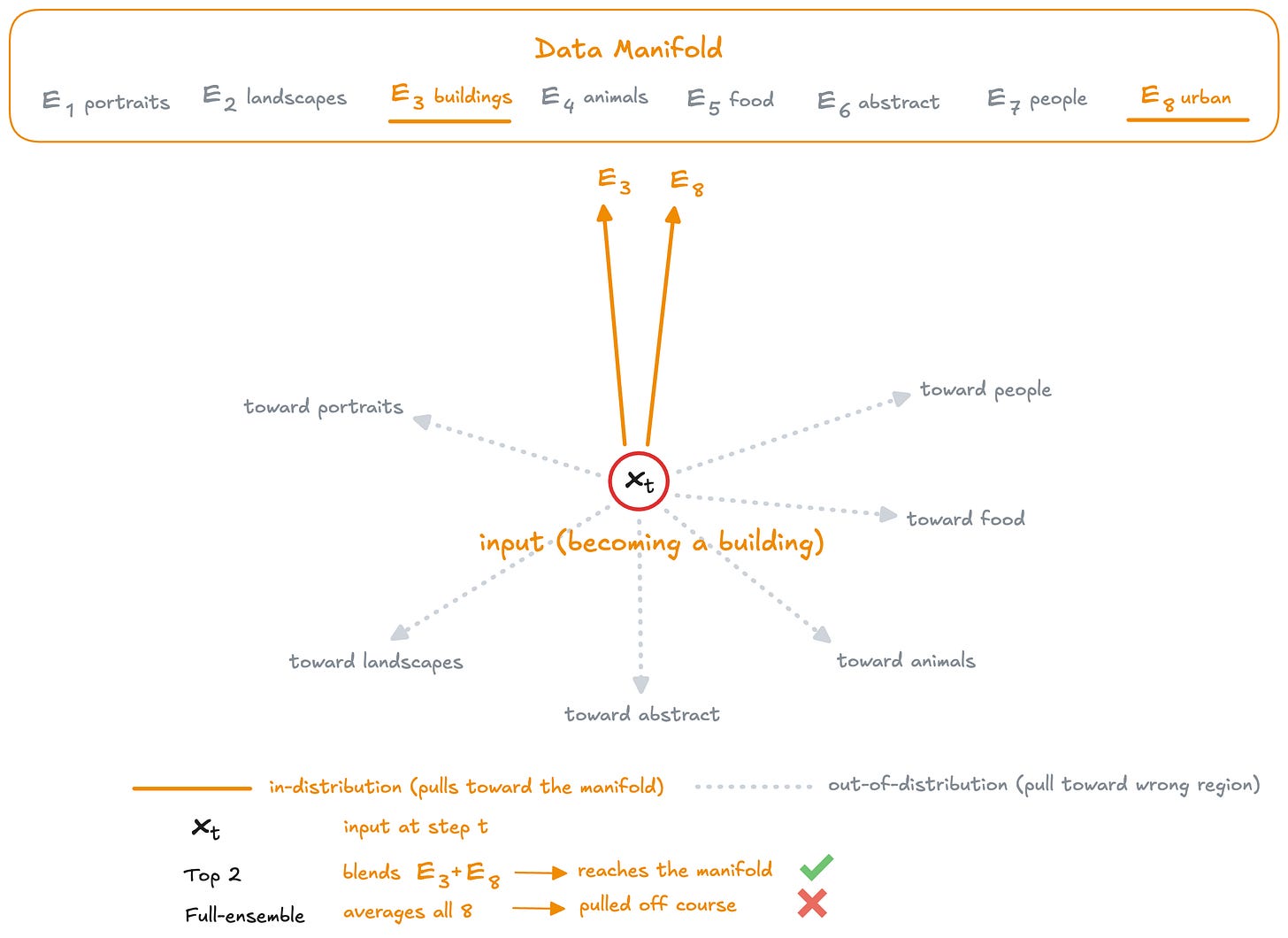
The answer is not in how smooth the path is, but where it leads. Full ensemble averaging reduces Jacobian spectral norms by cancelling variance across expert predictions, which is exactly why it wins on stability metrics. But each expert is trained on a disjoint data cluster. When all experts contribute to every input, most of them are producing velocity predictions for inputs that lie far outside their training distribution. The resulting velocity field is smooth because the out-of-distribution errors partially cancel, but it points toward a weighted average of all cluster centers rather than the data manifold.

In single-model diffusion, a smoother velocity field means cleaner integration means better samples. DDMs break this. The smoothing that lowers trajectory sensitivity is not coming from a better-conditioned ODE. It is coming from averaging contradictory predictions, which suppresses variance at the cost of introducing systematic bias away from any individual data cluster’s learned distribution. Sparse routing avoids this by selecting only the experts whose training data clusters are close to the current input in embedding space, keeping each active expert within its training distribution. The velocity field is noisier but points in the right direction.

We call this governing principle expert-data alignment. Generation quality depends on routing inputs to experts whose training clusters cover the current denoising state, even when doing so reduces the trajectory stability.

If expert-data alignment governs quality, 3 predictions should hold. Sparse routing should achieve higher alignment (selected experts have lower data-cluster distance). Selected experts should produce superior velocity predictions. And expert disagreement should correlate with quality degradation. We tested all three.

---

Experimental Validation

Cluster Distance Analysis

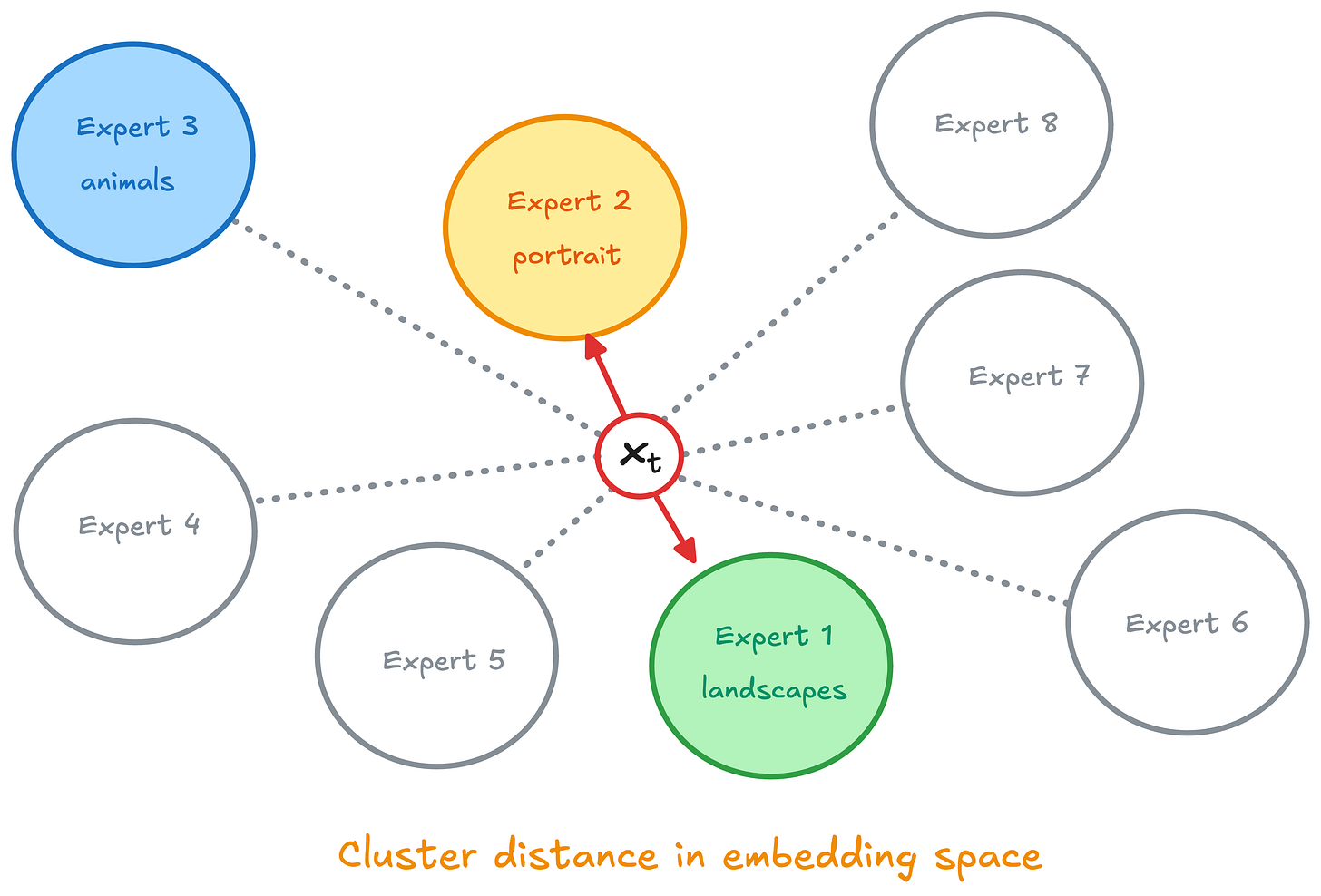
Does sparse routing actually select experts whose training distribution match the input?

Using the Paris DDM (K=8 experts, DiT-XL/2 architecture with ~606M parameters each), we extracted DINOv2-ViT-L/14 embeddings at timesteps t in {0.3, 0.5, 0.7} during sampling for 500 samples. For each state, we computed the Euclidean distance from the embedding to each of the 8 cluster centroids used during expert training, then ranked the experts by this distance.

\(\begin{array}{lcc} \hline \text{Routing} & \text{Mean Cluster Rank }\downarrow & \text{Top-2 Match Rate }\uparrow \\ \hline \text{Top-1} & 1.54 \pm 0.28 & 90.2\% \\ \text{Top-2} & 1.96 \pm 0.26 & 83.9\% \\ \text{Full Ensemble} & 4.50\ \text{(uniform)} & 25.0\%\ \text{(random)} \\ \hline \end{array}\)

The router consistently selects experts whose training distribution are closest to the current denoising state. Top-1 achieves a mean rank of 1.54 (near-optimal selection), while Top-2 maintains strong alignment at 1.96. Full Ensemble, by construction, averages across all experts regardless of relevance.

The router is picky, and that’s the point. Sparse routing filters out experts that are statistically likely to produce poor predictions because they’ve never seen similar data.

Per-Expert Prediction Quality

Do selected experts actually produce better predictions?

For each step in Top-2 generation, we computed velocity vectors from all experts and measured angular deviation from the final blended velocity (which successfully guides the image to completion).

\(\begin{array}{lccc} \hline \text{System} & \text{Selected Experts} & \text{Non-Selected Experts} & \text{Gap} \\ \hline \text{Paris (8 experts)} & 3.6^\circ & 5.1^\circ & 29\% \\ \text{MNIST (10 experts)} & 6.4^\circ & 11.3^\circ & 43\% \\ \hline \end{array}\)

Selected experts consistently produce predictions that align more closely with the successful trajectory. The gap widens with specialization: the MNIST system (each expert trained on a single digit) shows a 43% difference versus 29% for Paris. When experts are highly specialized, the cost of including an inappropriate expert increases. A landscape expert might still contribute useful texture when generating a portrait. A “zero” expert offers actively harmful gradients when drawing a “seven.”

Expert Disagreement Analysis

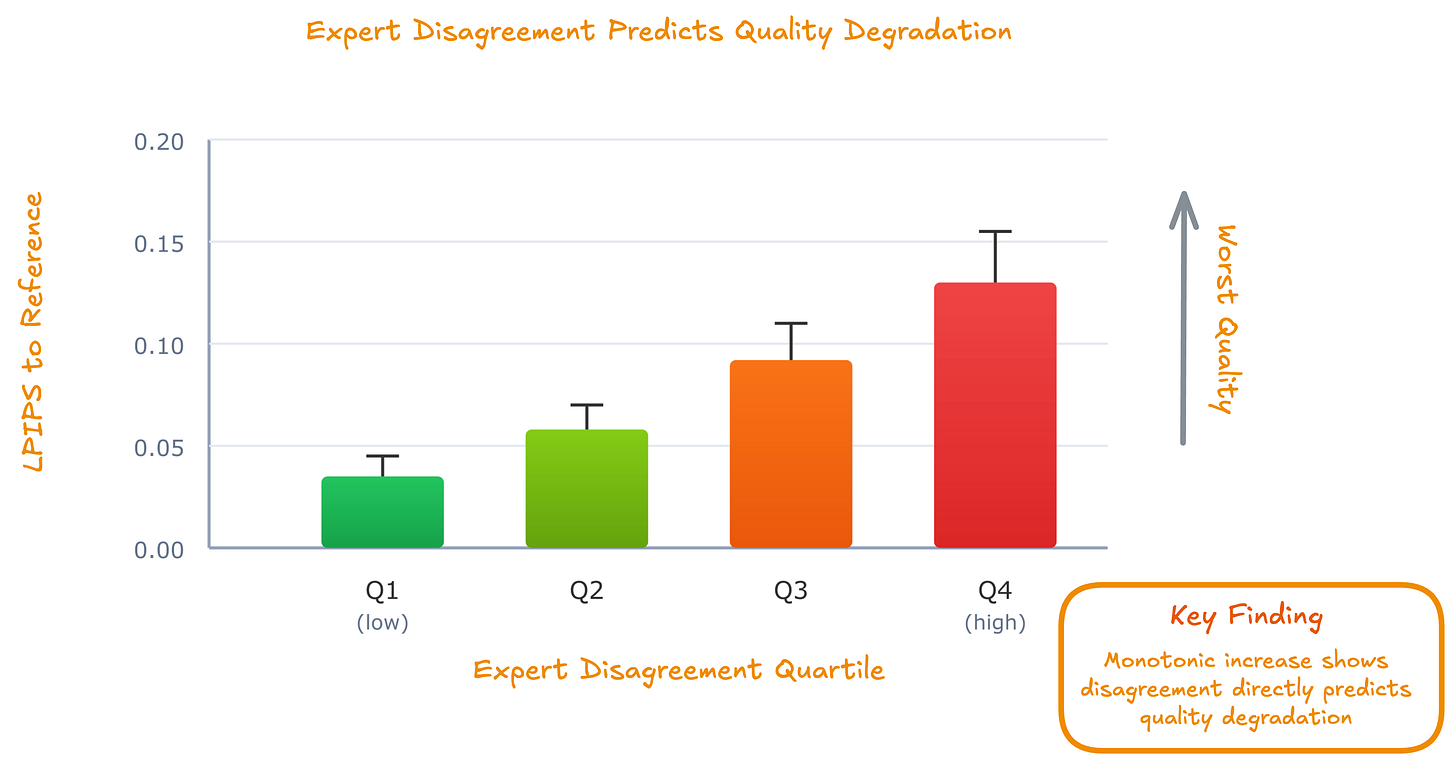
Does expert disagreement predict quality degradation?

We computed trajectory-integrated disagreement: the average pairwise Euclidean distance between expert velocity predictions, summed over the denoising trajectory. We sorted generated images into quartiles by disagreement and measured LPIPS (perceptual distance to reference).

Images in the high-disagreement quartile (Q4) exhibit worse LPIPS scores than those in the low-disagreement quartile (Q1). The relationship is monotonic.

This is the Full Ensemble failure mode. When experts agree, the average produces reasonable results. When experts disagree (which happens frequently because most experts are out-of-distribution), the average becomes an incoherent compromise. It’s like asking a portrait painter and a landscape painter to collaborate on a cityscape. Sparse routing avoids this by silencing experts that are likely to disagree.

---

Is Stability Still Useful?

If numerical stability doesn’t govern quality, is it still useful? Yes, but it just measures the wrong thing for generation quality.

Stability Measures Convergence, Not Correctness

Step-refinement disagreement measures whether the solver converges consistently. Full ensemble achieves excellent convergence with step-refinement disagreement approximately 0.020 - doubling the number of sampling steps barely changes the output. Top-2 exhibits more numerical noise with step-refinement disagreement approximately approximately 0.051.

But it’s possible to converge perfectly to a blurry, incoherent average. Stability metrics indicate how easily the solver finds a solution, not whether that solution is good.

Within-Strategy Diagnostics

Trajectory sensitivity may still work as a within-strategy diagnostic. If practitioners are using Top-2 routing, a sudden spike in sensitivity for a specific input might flag a “hard” sample that needs more inference steps, even though sensitivity doesn’t predict quality across routing strategies.

---

Discussion

Limitations

We validate our hypothesis on two DDM systems (Paris with 8 experts, MNIST with 10 experts). The pattern is consistent across both, but additional systems would strengthen the conclusions - in progress at Bagel Labs. The relationship between cluster distance and prediction quality could be confounded by other factors, such as experts trained on larger clusters being more robust. We control for this by using the same embedding space (DINOv2) that was used during expert training.

Implications

For practitioners building DDM systems:

1. Routing should prioritize alignment over stability. Standard numerical stability metrics don’t indicate system health in DDMs. A “smooth” sampler may simply be averaging away useful signal.

2. Sparse routing is preferable. Top-2 routing achieves a favorable tradeoff: it maintains expert-data alignment while allowing experts to cross-reference each other. Top-1 may be too aggressive; Full Ensemble destroys alignment.

3. Monitor expert-data alignment directly. Track data-cluster distance ranks and expert disagreement during development, not just final FID scores.

---

Conclusion

Numerical stability doesn’t govern generation quality in Decentralized Diffusion Models. Expert-data alignment does. It means routing inputs to experts trained on similar data.

DDM systems should be evaluated and optimized for alignment rather than stability. Sparse routing succeeds not because it produces stable trajectories, but because it ensures each active expert operates within its domain of competence.

---

This post presents findings from our research. For full experimental details, methodology, and additional analyses, see:

Expert-Data Alignment Governs Generation Quality in Decentralized Diffusion Models

@misc{villagra_expertdataalignment_2026,
  author       = {Marcos Villagra and Bidhan Roy and Raihan Seraj and Zhiying Jiang},
  title        = {{Expert-Data Alignment Governs Generation Quality in Decentralized Diffusion Models}},
  howpublished = {\url{https://arxiv.org/abs/2602.02685}},
  note         = {arXiv:2602.02685 • accessed DD Mon YYYY},
  year         = {2026}
}